삶의 공유
선형 회귀의 한계를 넘어서: 다항 회귀와 랜덤 포레스트로 비선형 데이터 정복하기 본문

현실 세계의 데이터는 언제나 깔끔한 직선으로 표현되지 않습니다. 주택 가격, 주식 시장, 혹은 생물학적 성장 곡선 등 많은 데이터가 곡선 형태의 비선형(Non-linear) 패턴을 띱니다. 이럴 때 단순한 선형 회귀 모델을 고집한다면, 우리는 데이터가 가진 중요한 정보를 놓치게 될 것입니다.
오늘은 선형 가정이 어긋날 때 대처할 수 있는 강력한 무기인 **다항 회귀(Polynomial Regression)**와 **랜덤 포레스트(Random Forest)**에 대해 깊이 있게 알아보겠습니다.
1. 다항식 항을 추가하고 다항 회귀 모델 훈련하기
선형 회귀가 데이터를 직선으로만 바라본다면, 다항 회귀는 데이터에 제곱($x^2$), 세제곱($x^3$) 항을 추가하여 모델이 곡선을 학습할 수 있도록 유연성을 부여하는 방법입니다.
사이킷런의 PolynomialFeatures 변환기 클래스를 사용하면 이차항($d=2$)을 추가하는 것이 매우 간단합니다.
예시 코드 구현
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
import numpy as np
import matplotlib.pyplot as plt
# 1. 데이터 생성
X = np.array([258.0, 270.0, 294.0,
320.0, 342.0, 368.0,
396.0, 446.0, 480.0, 586.0])[:, np.newaxis]
y = np.array([236.4, 234.4, 252.8,
298.6, 314.2, 342.2,
360.8, 368.0, 391.2,
390.8])
# 2. 모델 초기화
lr = LinearRegression() # 일반 선형 회귀 모델
pr = LinearRegression() # 다항 회귀를 위한 선형 모델
quadratic = PolynomialFeatures(degree=2) # 2차항 생성기
# 3. 데이터 변환 (이차항 추가)
X_quad = quadratic.fit_transform(X)
# 4. 선형 회귀 모델 훈련
lr.fit(X, y)
# ? np.newaxis 설명:
# 사이킷런은 입력 데이터가 항상 2차원 배열(행렬)이기를 기대합니다.
# np.arange()는 1차원 배열을 반환하므로, [:, np.newaxis]를 통해
# (N,) 형태를 (N, 1) 형태의 열 벡터로 변환하여 모델 입력에 맞춥니다.
X_fit = np.arange(250, 600, 10)[:, np.newaxis]
y_lin_fit = lr.predict(X_fit)
# 5. 다항 회귀 모델 훈련
pr.fit(X_quad, y)
# 예측할 때도 입력값 X_fit을 2차항으로 변환해서 넣어줘야 함에 주의하세요!
y_quad_fit = pr.predict(quadratic.fit_transform(X_fit))
# 6. 결과 그래프 그려보기
plt.scatter(X, y, label='Training points')
plt.plot(X_fit, y_lin_fit, label='Linear fit', linestyle='--')
plt.plot(X_fit, y_quad_fit, label='Quadratic fit')
plt.xlabel('Explanatory variable')
plt.ylabel('Predicted or Known target values')
plt.legend()
plt.tight_layout()
plt.show()

* np.newaxis의 역할 (효과)
이 명령어를 사용하면 **크기가 1인 새로운 차원(Axis)**이 생깁니다.
예를 들어, 데이터가 3개인 1차원 배열이 있다고 가정해 봅시다.
- 기존 (1차원): [1, 2, 3]
- 모양(Shape): (3,)
- 그냥 숫자 3개가 나열된 상태입니다.
여기에 [:, np.newaxis]를 적용하면?
- 변경 후 (2차원): [[1], [2], [3]]
- 모양(Shape): (3, 1)
- 3행 1열짜리 2차원 행렬(Column Vector)이 되었습니다.
즉, np.newaxis가 들어간 자리에 항상 숫자 1이 채워진다고 이해하시면 정확합니다.
왜 이렇게 할까요? (Scikit-learn을 위해)
사이킷런(Scikit-learn)의 모델들은 입력 데이터로 항상 '표(Table)' 형태의 2차원 행렬을 원합니다.
- 행(Row): 데이터 샘플의 개수
- 열(Column): 특성(Feature)의 개수
모델 성능 평가 (MSE와 R²)
그래프로만 봐도 다항 모델이 더 잘 맞는 것 같지만, 정확한 수치로 비교해 보겠습니다.
from sklearn.metrics import mean_squared_error
from sklearn.metrics import r2_score
y_lin_pred = lr.predict(X)
y_quad_pred = pr.predict(X_quad)
print('훈련 MSE 비교 - 선형 모델 : %.3f, 2차 다항 회귀 모델 : %.3f' %(mean_squared_error(y, y_lin_pred),
mean_squared_error(y, y_quad_pred)))
# 결과: 훈련 MSE 비교 - 선형 모델 : 569.780, 2차 다항 회귀 모델 : 61.330
print('훈련 R^2 비교 - 선형 모델 : %.3f, 2차 다항 회귀 모델 : %.3f' %(r2_score(y, y_lin_pred),
r2_score(y, y_quad_pred)))
# 결과: 훈련 R^2 비교 - 선형 모델 : 0.832, 2차 다항 회귀 모델 : 0.982
결과 해석: MSE는 크게 줄어들고 $R^2$는 1에 가까워졌습니다. 이는 다항 모델이 데이터의 패턴을 훨씬 더 잘 설명한다는 것을 의미합니다.
2. 주택 데이터셋을 사용해 비선형 관계 모델링하기
이번에는 실제 데이터인 주택 데이터셋(Housing Dataset)을 사용하여 '하위 계층 비율(LSTAT)'이 '주택 가격(MEDV)'에 미치는 영향을 모델링 해보겠습니다. 여기서는 2차항뿐만 아니라 3차항까지 추가해 봅니다.
# 데이터 준비 (df는 주택 데이터 데이터프레임이라고 가정)
X = df[['LSTAT']].values
y = df['MEDV'].values
regr = LinearRegression()
# 2차, 3차 다항식 특성을 만듬
quadratic = PolynomialFeatures(degree=2)
cubic = PolynomialFeatures(degree=3)
# 데이터를 변환
X_quad = quadratic.fit_transform(X)
X_cubbic = cubic.fit_transform(X)
# 시각화를 위한 X 범위 설정
X_fit = np.arange(X.min(), X.max(), 1)[:, np.newaxis]
# 1. 단순 선형 회귀 (d=1)
regr = regr.fit(X, y)
y_lin_fit = regr.predict(X_fit)
linear_r2 = r2_score(y, regr.predict(X))
# 2. 이차 다항 회귀 (d=2)
regr = regr.fit(X_quad, y)
y_quad_fit = regr.predict(quadratic.fit_transform(X_fit))
quadratic_r2 = r2_score(y, regr.predict(X_quad))
# 3. 삼차 다항 회귀 (d=3)
regr = regr.fit(X_cubbic, y)
y_cubic_fit = regr.predict(cubic.fit_transform(X_fit))
cubic_r2 = r2_score(y, regr.predict(X_cubbic))
# 결과 그래프를 그려보자
plt.scatter(X, y, label='training points', color='lightgray')
plt.plot(X_fit, y_lin_fit, label='Linear (d=1), $R^2=%.2f$' %linear_r2, color='blue',lw=2, linestyle=':')
plt.plot(X_fit, y_quad_fit, label='Quadratic (d=2), $R^2=%.2f$' %quadratic_r2, color='red',lw=2, linestyle='-')
plt.plot(X_fit, y_cubic_fit, label='Cubic (d=3), $R^2=%.2f$' %cubic_r2, color='green',lw=2, linestyle='--')
plt.xlabel("% lower status of ther population [LSTAT]")
plt.ylabel("Price in $1000s [MEDV]")
plt.legend(loc='upper right')
plt.show()

결과에서 볼 수 있듯이 선형과 이차 다항 모델보다 삼차 다항 모델이 주택 가격과 LSTAT 사이의 관계를 더 잘 잡아냅니다.
주의: 다항 특성을 많이 추가할수록 모델의 복잡도가 높아져 **과대적합(Overfitting)**의 가능성이 증가한다는 점을 꼭 기억해야 합니다.
PolynomialFeatures(degree=2)를 사용했을 때 수식이 어떻게 변하는지 단순 선형 회귀와 비교하여 직관적으로 설명해 드리겠습니다.
핵심은 **"입력 데이터($x$)의 개수를 뻥튀기해서 모델에게 곡선을 그릴 수 있는 능력을 주는 것"**입니다.
1. 특성이 1개일 때 (x)
가장 간단한 경우로, 예를 들어 '공부 시간(x)' 하나로 **'시험 점수(y)'**를 예측한다고 가정해 보겠습니다.
A. 선형 모델 (Linear Model)
단순히 직선 하나를 긋습니다.

- 설명: x(공부 시간)가 증가하면 y는 일정하게 증가하거나 감소합니다.
- 형태: 직선
B. 다항 회귀 모델 (Polynomial Model, degree=2)
PolynomialFeatures(degree=2)는 입력값 x를 받아서 x^2(제곱) 항을 자동으로 생성하여 추가합니다. 이제 모델은 x와 x^2 두 가지 재료를 갖게 됩니다.

- 설명: 중학교 때 배운 2차 함수(y=ax^2+bx+c) 꼴이 되었습니다.
- 형태: $U$자 모양이나 뒤집힌 U자 모양의 **곡선(포물선)**을 그릴 수 있게 됩니다.
- 효과: 데이터가 직선이 아니라 휘어있는 모양일 때 훨씬 더 잘 맞출 수 있습니다.
2. 특성이 2개일 때 (x_1, x_2) - 중요!
특성이 늘어나면 degree=2의 효과는 더 강력해집니다. 예를 들어 **'키(x_1)'**와 **'몸무게(x_2)'**로 무언가를 예측한다고 합시다.
A. 선형 모델

- 각 변수가 독립적으로 결과에 영향을 미칩니다.
B. 다항 회귀 모델 (degree=2)
PolynomialFeatures(degree=2)는 단순히 제곱만 하는 것이 아니라, **변수끼리의 곱(상호작용)**까지 모두 만들어냅니다.
생성되는 항: 1, x_1, x_2, x_1^2, x_2^2, x_1x_2
수식은 다음과 같이 변합니다:
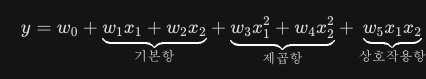
- x_1^2, x_2^2 (제곱항): 각 변수의 곡선 관계를 설명합니다.
- x_1x_2 (상호작용항): 이게 아주 중요합니다. "키가 크면서 동시에 몸무게가 많이 나가는 경우"와 같이 두 변수가 결합했을 때 나타나는 시너지 효과를 모델링할 수 있게 해줍니다.
또 다른 접근: 특성 변환 (Log Transformation)
무작정 다항식 차수를 높이는 것이 언제나 최선은 아닙니다. 경험과 직관을 바탕으로 데이터를 **로그 스케일(Log Scale)**로 변환하면, 모델을 복잡하게 만들지 않고도 선형 회귀 모델 성능을 높일 수 있습니다.
# 로그 변환 및 제곱근 변환 적용
X_log = np.log(X)
y_sqrt = np.sqrt(y)
# 변환된 데이터에 맞게 시각화 범위 재설정
X_fit = np.arange(X_log.min()-1, X_log.max()+1, 1)[:, np.newaxis]
# 선형 모델 훈련
regr = regr.fit(X_log, y_sqrt)
y_lin_fit = regr.predict(X_fit)
linear_r2 = r2_score(y_sqrt, regr.predict(X_log))
# 그래프 그리기
plt.scatter(X_log, y_sqrt, label='training points', color='lightgray')
plt.plot(X_fit, y_lin_fit, label='Linear fit, $R^2=%.2f$' %linear_r2, color='blue', lw=2)
plt.xlabel("log(% lower status of ther population [LSTAT])")
plt.ylabel("Sqrt(Price in $1000s [MEDV])")
plt.legend(loc='lower right')
plt.show()

3. 랜덤 포레스트를 사용하여 비선형 관계 다루기
랜덤 포레스트(Random Forest)는 선형 모델이나 다항 회귀와는 개념적으로 완전히 다릅니다. 이들은 데이터를 결정 트리(Decision Tree) 규칙에 따라 학습하기 좋은 작은 영역으로 분할하여 예측을 수행합니다.
결정 트리 회귀 (Decision Tree Regressor)
결정 트리의 가장 큰 장점은 데이터의 스케일(단위)에 영향을 받지 않으므로, 표준화나 정규화 같은 특성 변환이 필요 없다는 점입니다.
# ? lin_regplot 함수 설명
# 모델의 예측 경계선과 실제 데이터를 시각화해주는 헬퍼 함수입니다.
# model.predict(X)를 통해 모델이 학습한 회귀선을 그립니다.
def lin_regplot(X, y, model):
plt.scatter(X, y, c='steelblue', edgecolor='white', s=70)
plt.plot(X, model.predict(X), color='black', lw=2)
return
from sklearn.tree import DecisionTreeRegressor
X = df[['LSTAT']].values
y = df['MEDV'].values
# 깊이가 3인 결정 트리 모델 생성
tree = DecisionTreeRegressor(max_depth=3)
tree.fit(X, y)
# ? sort_idx 설명
# 그래프를 그릴 때 X값이 뒤죽박죽이면 선이 꼬여서 그려집니다.
# X.flatten().argsort()를 사용하여 X값을 작은 순서대로 정렬한 인덱스를 구합니다.
# 이 인덱스로 X와 y를 정렬해야 깔끔한 계단 모양의 회귀선을 그릴 수 있습니다.
sort_idx = X.flatten().argsort()
lin_regplot(X[sort_idx], y[sort_idx], tree)
plt.xlabel("% lower status of ther population [LSTAT]")
plt.ylabel("Price in $1000s [MEDV]")
plt.show()

결과에서 볼 수 있듯 결정 트리는 데이터의 일반적인 경향을 잘 잡아내지만, 예측선이 매끄럽지 않고 계단 모양을 띠는 것이 특징이자 한계입니다.
랜덤 포레스트 회귀 (Random Forest Regressor)
단일 결정 트리의 과대적합 문제를 해결하기 위해, 여러 개의 트리를 앙상블(Ensemble)한 랜덤 포레스트를 사용합니다. 무작위성이 모델의 분산을 낮춰주어 일반화 성능이 뛰어납니다.
from sklearn.model_selection import train_test_split
X = df.iloc[:, :-1].values
y = df['MEDV'].values
# 훈련/테스트 데이터 분리
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.4, random_state=1)
from sklearn.ensemble import RandomForestRegressor
forest = RandomForestRegressor(n_estimators=1000,
# ? criterion='squared_error' 설명:
# 트리를 분할할 때 사용할 평가 지표입니다.
# 회귀 문제이므로 '평균 제곱 오차(MSE)'를 최소화하는 방향으로
# 노드를 분할한다는 의미입니다. (구버전 'mse'와 동일)
criterion='squared_error',
random_state=1,
n_jobs=-1)
forest.fit(X_train, y_train)
y_train_pred = forest.predict(X_train)
y_test_pred = forest.predict(X_test)
print('훈련 MSE: %.3f, 테스트 MSE: %.3f' % (
mean_squared_error(y_train, y_train_pred),
mean_squared_error(y_test, y_test_pred)))
print('훈련 R^2: %.3f, 테스트 R^2: %.3f' % (
r2_score(y_train, y_train_pred),
r2_score(y_test, y_test_pred)))
# 훈련 MSE: 1.644, 테스트 MSE: 11.085
# 훈련 R^2: 0.979, 테스트 R^2: 0.877
잔차(Residual) 분석
모델의 성능을 시각적으로 진단하기 위해 잔차 플롯을 그려봅니다. 이상적으로는 잔차가 0을 중심으로 무작위로 분포해야 합니다.
plt.scatter(y_train_pred,
y_train_pred - y_train,
c='steelblue',
edgecolor='white',
marker='o',
s=35,
alpha=0.9,
label='Training data')
plt.scatter(y_test_pred,
y_test_pred - y_test,
c='limegreen',
edgecolor='white',
marker='s',
s=35,
alpha=0.9,
label='Test data')
plt.xlabel('Predicted values')
plt.ylabel('Residuals')
plt.legend(loc='upper left')
plt.hlines(y=0, xmin=-10, xmax=50, lw=2, color='black')
plt.xlim([-10, 50])
plt.tight_layout()
# plt.savefig('images/10_15.png', dpi=300)
plt.show()

결과를 보면 랜덤 포레스트가 타깃과 특성 간의 관계를 비교적 잘 설명하고 있지만, 훈련 데이터에 다소 과대적합된 경향도 확인할 수 있습니다.
📝 핵심 요약
- 다항 회귀 (Polynomial Regression): 단순 선형 회귀로 해결되지 않는 비선형 데이터를 다룰 때, 특성의 거듭제곱 항을 추가하여 모델링할 수 있습니다.
- 특성 변환의 중요성: 무조건 차수를 높이는 것보다 Log나 Sqrt 같은 변환을 통해 데이터를 선형적으로 만드는 것이 더 효율적일 수 있습니다.
- 결정 트리 (Decision Tree): 데이터 전처리가 필요 없지만, 과대적합의 위험이 있고 예측 결과가 계단 모양으로 불연속적입니다.
- 랜덤 포레스트 (Random Forest): 여러 결정 트리를 결합하여 과대적합을 줄이고 일반화 성능을 높인 강력한 모델입니다.
이 글은 [머신러닝 교과서 with 파이썬, 사이킷런, 텐서플로]의 내용을 바탕으로 학습하여 작성되었습니다.
'Data Scientist > ML' 카테고리의 다른 글
| [Deep Learning] 밑바닥부터 시작하는 다층 인공 신경망(MLP) 구현하기: MNIST 실습 (0) | 2025.12.11 |
|---|---|
| 정답 없는 데이터에서 보물을 찾아라! 머신러닝 군집 분석 (Cluster Analysis) 완벽 가이드 🗺️ (0) | 2025.12.09 |
| 회귀 분석으로 주택 가격 예측하기 — 단순 회귀부터 RANSAC까지 한 번에 이해하기 (0) | 2025.11.18 |
| [실전프로젝트] IMDb 영화 리뷰 감성 분석(2편) - 로지스틱 회귀 최적화 & 대용량 온라인 학습 (0) | 2025.10.27 |
| [실전프로젝트] IMDb 영화 리뷰 감성 분석(1편) - 텍스트 전처리와 BoW 모델 이해 (0) | 2025.10.20 |



